Teorija grafova

Kada u matematici spomenemo riječ graf svima je prva asocijacija dobro znani graf funkcija (naprimjer parabola u slučaju kvadratne funkcije), ali grana diskretne matematike pod nazivom teorija grafova proučava pojam grafa koji ima nešto drugačije značenje.

Teorija grafova je posebna grana Kombinatorike, ali je usko povezana s primijenjenom matematikom, teorijom optimizacije i računalnim znanostima. Sama motivacija za nastajanjem ove grane pokrenuta je s problemom Königsberških mostova.

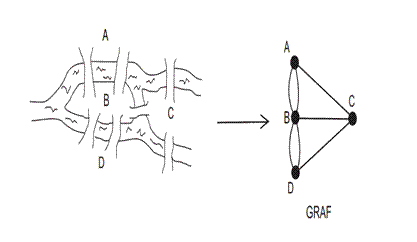
Stari pruski grad Königsberg smješten je na obalama rijeke Pregel. Dio grada smješten je na dva otoka koji su povezani s kopnom i međusobno sa sedam mostova, kako je prikazano na slici. Građani su se pitali postoji li način da obiđu čitav grad tako da prijeđu svaki most samo jednom. Odgovor na to pitanje dao je utemeljitelj teorije grafova Leonhard Euler (1707. - 1783.) godine 1736. kada je koristeći prikaz mostova u obliku grafa pokazao kako nije moguće obići čitav grad tako da se svaki most prijeđe samo jednom.

Kao što je prikazano na slici možemo vidjeti da su dijelovi grada označeni slovima te njih možemo smatrati vrhovima grafa i zapisati ih u obliku skupa V = {A, B, C, D} te mostove koji ih povezuju nazivamo bridovima i možemo zapisati u skupu E = {{A, B}, {A, B}, {B, D}, {B, D}, {A, C}, {B, C}, {C, D}.

Nakon motivacije i priče o utemeljenju teorije grafova i grafičkom prikazu možemo definirati sami graf.

Graf G je uređena trojka G = (V(G), E(G), ѱG) koja se sastoji od nepraznog skupa  V = V(G), čiji su elementi vrhovi od G, skupa E = E(G) disjunktnog s V(G), čiji su elementi bridovi od G i funkcije incidencije ѱG koja svakom bridu od G pridružuje neuređeni par (ne nužno različitih) vrhova od G.

Kao što je navedeno u definiciji skup V mora sadržavati barem jedan vrh, dok skup E može biti i prazan skup. Tako da i jedna točka označava graf. Nadalje, skupovi V i E ne moraju biti konačni, a ukoliko su oba konačna tada graf G nazivamo konačnim grafom. Također unutar grafa moguće je da su dva različita vrha spojena istim bridom i tada kažemo da graf sadrži višestruke bridove, a ako unutar grafa postoji brid koji spaja vrh sa samim sobom kažemo da graf sadrži petlju. Klasu grafova koji ne sadrže niti višestruke bridove niti petlje nazivamo Jednostavni grafovi. Klasu grafova koji sadrže  višestruke bridove, ali ne i petlju nazivamo Multigraf dok grafove koji sadrže i barem jednu petlju nazivamo Pseudografovi.

Također važni pojmovi za proučavanje grafova jesu stupanj (valencija) vrha koja predstavlja broj bridova povezanih s promatranim vrhom V te obojivost grafova koja nam govori koji je minimalan broj boja s kojima je moguće obojati vrhove grafa tako da svaka dva susjedna grafa budu obojeni različitim bojama.

Specijalni grafovi:

●      Prazan graf je graf u kojem nema bridova.

●      Povezan graf je svaki graf u kojem postoji put između bilo koja dva vrha u grafu.

●      Ciklus s n vrhova predstavlja graf kojemu je početni vrh jednak završno.

●      Potpun graf je jednostavan graf u kojem je svaki par vrhova spojen bridom. Oznaka za potpun graf s n vrhova je Kn.

●      Bipartitan graf je graf čiji se skup vrhova može podijeliti u dva skupa X i Y tako da svaki brid ima jedan kraj u X, a drugi u Y . Particija (X, Y) zove se biparticija grafa.

●      Stablo je povezan graf koje ne sadrži niti jedan ciklus.

●      Neusmjereni graf - graf kojem brid ide u oba smjera, odnosno možemo čitati da za u,v ∈ V(G) brid e ∈ E(G)  spaja vrh u s vrhom v i obratno.

●      Usmjereni graf - bridovi grafa koji povezuju vrhove označeni su strelicama kako bi se naglasilo da je smjer kretanja točno određen pa tako za razliku od neusmjerenog grafa  za u,v ∈ V(G) brid e ∈ E(G)  spaja vrh u s vrhom V, ali ne i obratno.

●      Težinski graf - usmjeren graf kojem bridovi dodatno imaju svoju težinu koju nazivamo kapacitet. Ovakvi grafovi se najčešće koriste u problemima optimizacije.

●      Snark - je graf u kojemu je svaki vrh stupnja tri te ga nije moguće obojati s tri boje. Zanimljivost ove vrste grafova jest što je njihovo postojanje pokazao hrvatski matematičar Danilo Blanuša, a naziv Snark  motiviran je pjesmom  Lewisa Carrolla The Hunting of the Snark.

Kada je riječ o primjeni grafova navest ćemo neke najpoznatije probleme u kojima se koristi struktura grafova, a koji su riješeni uz pomoć grafova ili čiji se prikaz modelira grafom:

●      Problem četiri boje - može li se bilo koja karta obojiti najviše četirima bojama tako da susjedne države budu različito obojene?
Ovaj je problem prvi postavio britanski matematičar Francis Guthrie 1852. godine. Naizgled jednostavan problem, koji je danas poznat kao dokazani teorem o četiri boje nije bilo lako dokazati te je jedan od prvih problema koji je dokazan računalno tek 1976. godine, a jednostavniji dokaz ponuđen je 1997. godine.

●      Problem trgovačkog putnika - jedan od poznatih problema u računarstvu u kojem se želi pronaći optimalan put tako da trgovac obiđe n gradova, svaki točno jednom, i na kraju se vrati u početni grad.

●      Network flow problemi - klasa problema koji primaju težinski graf koji reprezentira neki optimizacijski problem.

○      naprimjer - opskrba poljoprivrednog obrta s vodom gdje je svaki vrh mjesto kojem je potrebna voda ili mjesto gdje se voda može čuvati, a bridovi su putevi kojima voda dolazi te su njihove težine trošak same vode, cilj je pronaći put koji će poljoprivrednika najmanje koštati, a da voda dođe do svih dijelova u kojima je potrebna.

I u kemiji možemo naći neke zanimljive primjene iz teorije grafova. Kako da sustavno poveže vrelišta alkana s njihovom strukturom (konstitucijom), prvi se dosjetio 1947. godine američki kemičar Harry Wiener. Došao je naime na zamisao da zbroji sve udaljenosti, izražene kao broj kovalentnih veza između ugljikovih atoma u molekuli ugljikovodika, pa da onda taj broj (zbroj) korelira s njihovim vrelištem. Dobiveni je broj nazvao “brojem putova” (path number), a definirao ga je kao “sumu udaljenosti između bilo koja dva ugljikova atoma u molekuli, u smislu najmanjeg broja veza između dva ugljika. To je bila vrlo osebujna primjena topološke analize (teorije grafova) u kemiji, jer se dotada kemijska teorija grafova primjenjivala samo za prebrojavanje izomera. Više o tome možete pročitati u znanstvenom članku dr.sc. Nenada Raosa putem linka https://doi.org/10.15255/KUI.2015.039.

Teorija grafova možda nije toliko poznata onima koji nemaju velik kontakt s  primijenjenom matematikom, teorijom optimizacije i računalnim znanostima, ali s obzirom na mnoštvo primjena i problema u kojima se koristi smatramo da je nadasve vrlo zanimljiva grana matematike. Nadamo se da smo vam uspjeli prenijeti barem mali dio zanimljivosti i zainteresirati vas da dodatno proučite nešto više o ovoj vrsti grafova.

Vaša eMatematika